First, I hypothesized in the last post that the positive relationship between current and flux estimator offset (with respect to the Hall effect sensors), seen here, was due to underestimated inductance. At high current, the rotor electrical angle predicted by the flux estimator would lead the angle interpolated from the Hall effect sensors, which I trust to be more accurate. Based on this figure, if the inductance parameter is too low, the [-IL] vector will be too short and the estimated flux vector will lead the actual flux vector at high current.
To test this, I changed only the L parameter in the sensorless code definitions, from 200μH to 300μH, leaving all other settings the same. After another 15-minute outdoor test drive, I plotted the flux estimator offset as a function of current once again. Here it is with the old data for comparison:
The effect is exactly what I thought it would be, flattening out the slope so that the offset is constant (near zero) though the entire range of load currents. I may have even gone a bit too far, creating a very slightly negative slope. But now I know that the inductance parameter has as predictable effect. The lead induced by using an inductance parameter that was 33% too low was about 20º electrical at maximum current. The error sensitivity is easy to predict using the vectors in this figure, but I will spare you the analysis in this post.
A closed-loop flux observer, which some day in the future I will certainly try out, would seek to minimize the effect of an over- or under-estimated inductance parameter. The ultimate goal would be plug-and-play sensorless that adapts to any motor on the fly. But for now, I can live with nicely-behaved dependencies like this. Though, without the parallel-processed Hall effect sensor data, I would be lost as to how to characterize any of it.
I also tried out the sensorless controller on a different motor:
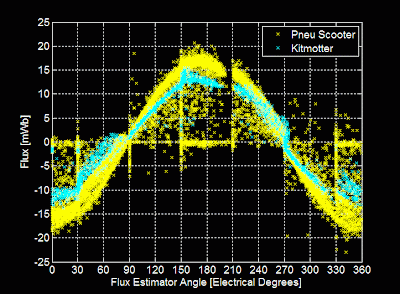
The thing clamped to the table is Kitmotter, a demonstration motor with very similar characteristics to Pneu Scooter's wheel motor. They have virtually the same measured inductance. Kitmotter has a higher resistance, which I modified in the sensorless code definitions for this test. It also has a lower torque constant, which is not an explicit parameter in this sensorless algorithm. What it does mean, though, is that the flux magnitude should be lower:
And in fact it is, by a small amount. It's also interesting to see that the general form of the flux estimates is very similar for both motors. In particular, the gap between about 200º and 210º shows up in both cases. This eliminates the possibility that the gap is caused by some asymmetry in one motor's winding. It could be current sensor asymmetry, though.
Kitmotter also accidentally allowed me to test the fast overcurrent shutdown. The dangling mess of alligator clips seen above was not the best idea, and when two of the phase outputs shorted to each other, causing a large spark, the controller shut down properly and gave an overcurrent fault. No dead FET.
The next parameter I want to tweak is the low-pass filter time constant, which affects the low speed performance of the sensorless control. I mentioned that the low-pass filter causes the flux estimator to lead the true angle at low speeds, and showed the offset as a function of speed. Here it is again, but in pseudo-3D:
 |
| Is this nauseating? |
Below 200rpm, the flux estimator angle is greater than the Hall effect sensor angle (trusted to be the true electrical angle). This causes the data, which should lie on the x = y plane, to slope off to the left at low speeds. Making the low-pass filter time constant longer should flatten out the plane and improve the low-speed torque. A lower "valid data" speed for switching to sensorless control will make start-up ramping, when I get around to that, just a bit easier.
I'm also worried about high-speed operation, which was the problem that magically disappeared when I made several code improvements. But, I'm still working with relatively slow motors, having commutation frequencies of 200Hz or less. I'm interested to see how things change (probably for the worse) when I try to run a non-direct-drive (indirect-drive?) motor like that of tinyKart, which can hit 750Hz or more.
More testing to come...



From what I've read, the benefits of FOC kinda go away when you go to higher commutation frequencies. We tested some higher Kv motors where the Back EMF was basically trapezoidal already so using simple sensorless commutation seemed much more appropriate. Then again I'm talking commutation frequencies of 3kHz-5kHz. One thought might be to actually use a phase lookup table that is shaped like the measured backEMF of your motor rather than using strictly a sine wave. I haven't found anyone or any literature suggesting that before.
ReplyDeleteIt definitely doesn't make much sense to try to control sinusoidal quantities at 3-5kHz with a 16kHz control loop and PWM frequency. And pushing to higher switching frequencies has its own downsides, so in that sense I agree. Block commutation is simple enough to run at high speeds. And at those speeds, the motor's inductance should filter most of the high harmonics out anyway, so it doesn't matter as much what the voltage and back EMF waveforms are. The current becomes sinusoidal anyway.
ReplyDeleteThe increased phase lag at high speeds might be one reason why FOC could be useful. The reactive component of the motor's impedance gets to be very large, so it's important to advance the timing to keep up. Maybe a simple open-loop phase advance table with block commutation is sufficient, though. I know a lot of RC controllers do something like this. FOC does this automatically but it's closed-loop, so it's only as good as the loop speed permits.
I like the idea of using the measured backEMF waveform as a lookup table. It's definitely something I've considered, but I haven't seen any examples either. It's more conducive to the closed-loop flux observer, where you can use that and the applied voltage to predict the current, and feed back the error between that and the measured current.
I wonder if the gap in the data could be due to some integer arithmetic (or an array index) overflowing or wrapping? I doubt that it is a current sensor problem since the motors probably don't draw the same current, but the gap occurs at the same phase angle.
ReplyDeleteI've definitely had problems with integer math overflowing, so I should carefully check the code again. The math should be symmetric across all three phases so I don't know why it would overflow only in one segment. But it's worth looking through carefully.
ReplyDeleteI was thinking something more along the lines of an asymmetric gain in one phase's current sensor. I did not calibrate them individually. (Although they do have individual zeros.) They're Hall effect current sensors so they are sensitive to external fields.