In a somewhat drastic attempt to force myself to get work done, I have decided not to ride
Pneu Scooter until I implement sensorless field-oriented control on its controller, a
3ph 3.1 board that's been happily commutating the motor off Hall effect sensors for something like 2-3 million electrical cycles. It's pretty much an ideal test platform since the motor is well-characterized (I built it.) and the controller is known to be reliable. It's also a relatively low-frequency system (175Hz at top speed), so the sensorless algorithm need not be absurdly fast to keep up with the commutation frequency. But, I do plan to use this algorithm on faster motors, so I'm designing for higher frequencies anyway.
The highest frequency the controller could run at is the PWM frequency, in this case 15.6kHz. Above this speed, it's not possible to update the commanded voltage to the motor fast enough, since the PWM duty cycle is not latched into a timer until the next PWM cycle. So, even if you could run a sensorless algorithm faster, there would be almost no point.
Back when I was using the
MSP430F2274, I ran a "fast loop" at 14.4kHz (PWM frequency) to handle sensor polling, speed estimation, position interpolation, and updating the three phase motor PWMs from a sine look-up table. The "slow loop" ran at 122Hz and handled current sampling, coordinate transformation into the rotating reference frame, and feedback control of the q-axis and d-axis currents.
 |
| This. |
On that processor, which doesn't have a hardware multiplier, getting the fast loop to run at 14.4kHz was a major challenge. I spent a large portion of the development time just optimizing the software using
a number of tricks to get the processing time down to 53μs (for two motors). The largest single processor burden, accounting for 10μs, was the integer division required to get the speed of the motor, 1/(time per cycle). This was large enough that I couldn't compute both motor speeds in the same fast loop cycle; one always got priority.
 |
| High = processor in use. Low = processor free. The lighter portion of the trace is the single integer division. |
Even totally optimized with all integer math (no floating-point), the dual FOC was just barely able to fit in the fast loop at 14.4kHz. The leftover processor time went to the slow loop, which could be run arbitrarily slow thanks to the coordinate transformation to the rotating frame. So, having floating-point controller math in the slow loop has never been an issue.
But now, I've moved on to the
STM32F103 32-bit ARM processor, which has a hardware multiplier. Though so far I haven't done anything other than
waste the extra processing power on silly things, one of my motivations for giving up my beloved MSP430 was to be able to implement sensorless field-oriented control. But first, for comparison, here's what single-motor FOC code looks like ported to the STM32F103:
The fast loop on this processor runs at 10kHz. It's no longer tied to the PWM frequency, so it's easy to change. I chose 10kHz for simple math. Using the same clock speed as the MSP430, single-motor FOC takes just under 7us. The integer operations, including multiplication, happen in one clock cycle instead of the 50-60 it took on the MSP430. Integer division is also fast, though to the best of my knowledge it isn't single-cycle. And these are 32-bit operands, so they inherently have more precision than the MSP430's 16-bit integers.
What about floating-point? I thought maybe the fast integer hardware would be leveraged somehow to make floating-point operations faster as well, even though the STM32F1-series does not have a hardware floating-point unit. So, I threw on my first attempt at a rotor flux observer, all implemented in floating-point math, to test this.
Mathematical Tangent:
The rotor flux observer, used to estimate the position of the rotor magnets in lieu of Hall effect sensors, is a simple one that I mentioned before:
It's an open-loop rotor flux observer, meaning there is no feedback to correct the estimated flux. It relies on a reasonably accurate estimate of R and L (the motor resistance and inductance, respectively) to produce the flux estimate. I did a little more thinking and decided that this is a good place to start, instead of jumping right into closed-loop flux observers. The nice things about the open-loop rotor flux estimator, in my view, are:
- It's very obvious what it's doing, in the context of the motor electrical model. In my experience, simple things tend to work more reliably.
- It estimates flux, instead of back EMF. The value of flux is speed-independent, so the amplitude of the flux estimate should remain constant. The integrator also filters out noise in the current measurement. No derivative of current is required.
- The effect of parameter offset is easy to analyze. More on this in a later post, but it's easy to show with simple geometrical arguments what the effect of an improperly-set R or L is.
I think in time I will move back toward the closed-loop observer, which can compensate for the parameter offset automatically, but for now this is what I'm starting with. So, the fast-loop code must sample the phase current sensors and the DC voltage. Phase voltage is computed as a duty cycle fraction of the DC voltage, based on the sine look-up table. The integration is implemented as a low-pass filter, to kill off DC offset.
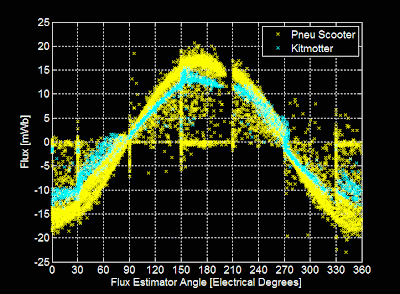
All three phase fluxes are estimated, and used to establish the motor position through what I will call "virtual Hall effect sensors" that detect flux zero-crossings. This method, though completely non-traditional and probably stupid, allows me to tape the flux observers to the back of my existing sensor-based FOC code and get up and running quickly.
Okay back to software:
Implementing the above open-loop flux estimator in all floating-point math was a terrible idea:
It looks like the processor utilization is 99%, but it's actually more like 120%. The 10kHz loop took so long that it actually took 120μs to finish each cycle...so I'm not even sure if it really finished or if the interrupt controller just gave up. The flux observer alone took about 80μs to run. I determined that each floating point multiply was taking about 7.44μs, or close to 120 clock cycles at 16MHz. So clearly the floating point math is still being done in software, and it's not really leveraging the hardware multiplier at all to speed things up.
So began a day or two of modifying the code to run faster without actually changing what it does. Software optimization is probably one of the most thankless tasks ever, since you make something work the same way it did before and nobody can see the difference. But I still find it somewhat fun to try to squeeze every bit of time out of a control loop.
First, I now have the ability to stick all my state variables into 32-bit integers and use the extra precision to make up for the lack of floating point capability. For example, instead of Phase A's current being represented in software as 38.7541723[A], it can be 38754[mA]. I don't care about sub-mA precision, and that still leaves me plenty of multiplication overhead. By that I mean I can still multiply the current, which fits in 17-bits of signed int, by up to 15 bits of precision without overflowing the 32-bit signed int.
For example, the floating-point current scaling would have been:
float raw_current, scaled_current;
raw_current = adc_read(CH) - offset;
scaled current = raw_current * 0.0561;
This scaled the raw ADC value to physical units of Amps. But it has more final precision than is really necessary and can be replaced with all integer math:
signed int raw_current, scaled_current;
raw_current = adc_read(CH) - offset;
scaled_current = raw_current * 561 / 10;
Now the scaled current is an integer value in mA. The intermediate precision required is about 22 bits. (12 bits for the raw ADC value plus 10 bits for the scaling operand 561.) The integer division by 10 is fast, and the precision is high enough that the truncated result is still perfectly fine.
After thus converting all the floating-point operations to integer math, the fast-loop consisting of FOC, ADC sampling, and flux observer was down to 50.5μs at 16Mhz:
This would already be good enough to run, but there are several other processing efficiency tricks I had ready to deploy. One obvious target for efficiency improvement is the ADC sampling. The STM32F103, like many other microcontrollers, uses a
Successive Approximation Register (SAR) ADC, which is sort-of like a guess-and-check process for converting an analog value to digital representation. Each guess takes time, so many cycles are spent waiting for the conversion to complete. As implemented above, the processor would just sit there waiting for the sample to finish.
With the ADC settings I have been using, each sample takes 4.55μs. The fast loop samples four analog channels, taking a total of 18.2μs. For most of that time, the processor is waiting for the ADC to finish. It doesn't need to be, though, since the ADC can run on its own and trigger an interrupt when it's done converting. Implementing this was straightforward: I have the fast loop code start the ADC and then have it cycle through five samples on its own. After each sample, the ADC interrupt retrieves the data and moves on to the next sample. While waiting for the ADC, the processor returns to the main loop.

This showed only marginal improvement. The total processor utilization is still about 50%, because the idle time saved by not waiting for the ADC is offset by extra processing time to decide what to do with the data. The result is that each sample now takes about 8μs, four of which is spent converting and four of which is spent decided what the data is and where to put it. The data manipulating part can be completely eliminated by using yet another hardware feature of this processor, the Direct Memory Access (DMA) peripheral. The ADC can tell the DMA to automatically transfer data to a specified memory location, with no processor involvement. This would completely automate the sampling, and bring the total processing time for the fast loop down to about 28μs.
But, there's also another way to squeeze even more horsepower out of the STM32F103. The clock speed can be multiplied by an on-board
Phase-Locked Loop (PLL) to up to 72MHz. (Right now, the 16MHz oscillator sets the clock speed directly.) I've never even bothered to try turning on the PLL, but now seemed like a good time to see what it would do. For some yet-unknown reason, I was only able to multiply my 16MHz oscillator by as much as 3.5 (or rather, divide it by two and then multiply it by seven...don't ask). That gives me 56MHz. I'm not sure why it won't go higher than that, but I suspect some hidden clock speed limit on a peripheral. But I tracked down all the obvious ones, and none were overclocked. Anyway, here's what the fast loop processor utilization looks like at 56MHz:

The entire FOC and flux estimator now take only 8μs. The ADC samples still take about 4μs, but the amount of that time spent processing data is greatly reduced. (The sampling time itself is limited by the ADC's peripheral clock speed limit of 14MHz, but the data manipulating time is based on the system clock.) The total processor utilization is now about 20%, leaving room for increasing the fast-loop rate or doing more processing for a closed-loop observer.
For now, though, I'm satisfied that the flux observer will run happily at 10kHz and I'm merging it with the FOC code I already have. Hopefully I will get to test it before Thanksgiving.