And now for something entirely different...

It's been a long time since I built something that isn't a robot, a motor controller, an electric vehicle, or a multirotor. Also, the Edgerton Center Summer Engineering Workshop (responsible for the DIY Segway, BWD Scooter, Cap Kart, and tinyKart) isn't running this year, so I feel the need to take on a summer project of my own. Inspired by the work of MITERS regulars Tyler, Daniel, Bayley, and Ggy, I'm attempting to build...

A Tesla Coil! (Sparks may or may not be added in MSPaint.)

Specifically, I'm building a Dual-Resonant Solid State Tesla Coil (DRSSTC). Tesla coils generate high voltage and pretty sparks using electromagnetic induction. They're loosely-coupled air-core transformers where the world is your output load. (Or just the toroidal "top load" and the air around the Tesla coil.) "Dual-resonant" implies that both the primary and the secondary form RLC series resonant circuits, tuned to about the same natural frequency. "Solid state" implies that the primary circuit is driven (near resonant frequency) by transistors, usually IGBTs although I will be starting with MOSFETs.

DRSSTCs appeal to me because they are are electrically and mechanically simple, but require good control to work properly (kind of like brushless motors). I'm too stubborn to go research DRSSTC controller designs, so instead I am forcing it to look as much like a motor controller as possible so I can use parts and techniques with which I'm already familiar. SSTCs are also the type of coil that can play music! Since I sacrificed MIDI Scooter's processing power in order to implement sensorless FOC, this can take its place.

Since this is my first ever Tesla coil build, I don't expect things to work properly and I don't expect amazing performance. I would be quite satisfied with mediocre sparks but really cool MIDI playing. If you want to learn the right way to design high-power, high-performance coils, I suggest following one of the links above to experienced coilers. Everything here should be considered experimental, at best, and for informational purposes only. With that said, here's the plan:

• The Secondary
• The Primary
• The Coupling
• The Driver
• SPICE Sims

Note: Throughout the design, I used three different methods to compute important electrical parameters of the coil. First, you can find formulas online for just about every part of a Tesla coil. The notation changes from one source to the next, but mostly they have the same formulas. The formula list I found easiest to use was from this page from teslacoils4christ.org. Second, there are also online calculators that let you calculate parameters for the entire coil at once, such as JavaTC. Lastly, I used a tool that has come in handy for motor design, FEMM, to estimate the parameters using finite element analysis. I cross-checked the results against each other and, if they were in agreement, I took an average.

The Secondary:

Starting with the secondary makes sense, since it's the geometric constraint that determines the overall size of the coil. In keeping with my motor controller / vehicle analogy, this is like choosing the size of the wheels and the mass of the car first, before worrying about what motor and controller to use. And just like the wheels, it's where the power exits the system and goes into the outside environment. Fitting, then, that some of the smaller coils around here use tire inner tubes as secondary top loads.

The secondary coil and the toroidal top load go together, creating a lightly-damped RLC circuit that determines the resonant frequency of the coil. I chose to target a relatively low resonant frequency so that I could drive the coil with gate drivers that I have experience with from motor controllers. More on those below, but for now the frequency I am targeting is 150kHz. I know from rough comparison to other coils in MITERS that I need something medium-sized (as opposed to big or small) for this frequency.

Toroid:

Starting with the toroid, I chose 5in diameter aluminum duct hose (McMaster PN 55335K43) as a reasonable size. Bending this around to a 14in average diameter (9in ID, 19in OD) makes a toroid which looks to have a reasonable shape, by eye. The important parameter of the toroid is its electrical capacitance. Time to fire up the three calculation methods for the first time:

TCFormulas: 21.1pF
JavaTC: 21.3pF
FEMM: 23.5pF
Average: 22.0pF

Since it's the most general and interesting method, I should explain how I got the capacitance value from FEMM: First, I start an electrostatics problem and set the Problem Type to "Axisymmetric" so that I can draw the toroid as if it were sliced by a half-plane and the solver will assume this slice is revolved around 360º. Then, I assign some properties: 0V/ground for the bottom border, 100kV for the toroid itself, air everwhere else. FEMM generates a mesh of triangles and solves for the voltage in the space around the toroid. It can also calculate the charge stored on the toroid.

Dividing the charge by the voltage gives the capacitance (C = Q/V). Because FEMM imports the coil geometry directly, it can calculated capacitance more generally than a simple formula. It includes the ground plane and could include a ceiling, other materials, primary conductors, and other things that might change the capacitance. Or, non-toroidal top loads. The other cool thing about having the exact geometry in FEMM is that you can match up the output image to the CAD solid model and see what it all looks like together (see below).

Secondary Coil:

The secondary coil is an air-core solenoid with lots of turns of relatively small wire. (It's the high-voltage, low-current side of the transformer.) I chose 28AWG wire because there's a ton of it lying around, it should be fairly easy to wind, and it should be able to handle a good amount of secondary power. With a coil length of 20in and a wire outer diameter of 0.014in, this gives 1,429 turns. This is probably a slight overestimate, since the inter-turn spacing will likely be a bit larger than one wire diameter on average. I have no intention of counting every single turn, but I might take a turns/in measurement later and readjust some numbers using that.

I'm using 4in ID PVC pipe as the coil form, so the coil diameter will be the OD of the pipe, 4.5in. The total length of wire will be 1,683ft. Based on my favorite wire gauge table, this will have a resistance of about 109Ω. The table also lists an ampacity of about 1.4Arms and a maximum frequency for 100% skin depth of 170kHz, above the target resonant frequency for this coil. So, it should be able to reach full ampacity. The standard formula for the inductance of a solenoid gives a value of 51.8mH for this coil. Here's what the other three calculation methods have to say:

TCFormulas: 46.9mH
JavaTC: 47.6mH
FEMM: 47.6mH
Average: 47.4mH

The formulas, calculators, and FEMM seem to take into account fringing at the ends of the solenoid, so they give a more consistent and hopefully more accurate estimate of the inductance than the ideal solenoid formula does. In FEMM, I imported the coil geometry from a .DXF file into a magnetics problem this time. This is the problem type I am more familiar with from motor design. After changing to an "Axisymmetric" problem, I assigned 1,429 turns of 28AWG to the secondary coil area and set it to 1A. FEMM produces the flux distribution and calculates the flux linkage for the coil:

The inductance is the flux linkage, in Webers, divided by the current, in Amps (L = λ/I). FEMM also confirms the coil resistance by showing the resistive voltage drop at 1A of 110V.

Resonance:

When the secondary coil and the toroid are connected in series, they form a lightly-damped RLC circuit with a natural frequency of 1/[2π*sqrt(L*C)]. Assuming the secondary coil has no capacitance of its own, the L and C values are exactly those from above and the natural frequency evaluates to 156kHz. The coil has some parasitic capacitance, though, and JavaTC suggests that the total secondary capacitance is closer to 26.0pF. I didn't attempt to validate this in FEMM, since the secondary coil capacitance is distributed along the entire length of the coil. However, using the total capacitance suggested by JavaTC, the natural frequency evaluates to 143kHz. Both are close enough to the 150kHz target to be acceptable.

It would also be interesting to know how sharp the resonant peak is - the Q value. This value would determine how much voltage amplification is possible at resonance, and how wide the frequency band of the resonant peak is. To get a feel for this, I put the R, L, and C values into a bode plot:

The resonant peak is at 143kHz and the voltage amplification at resonance is 50dB. The peak is quite narrow. The window for 40dB (100x) amplification is less than 1% in either direction away from resonance. The window for 20dB (10x) amplification is more forgiving, allowing about 5% deviation in either direction. Still, a hard target.

The Primary:

The primary circuit is also an RLC series resonant circuit consisting of a spiral-wound coil that forms the transformer primary, a capacitor bank, and the parasitic resistances of both. In a DRSSTC, the primary circuit's resonant frequency should be tuned to be nearly equal to the secondary's resonant frequency. "Tuning" involves changing the primary inductance by selectively tapping off the spiral coil in different locations.

Primary Coil:

The primary coil consists of a small number of turns of relatively large wire. (It's the low-voltage, high-current side of the transformer.) I chose 8AWG grounding wire for the coil. I don't think the gauge actually means much in this case, since the skin depth at 150kHz is something like 0.17mm. Only the outer layer of wire will be conducting current, so the effective resistance will be higher than a normal 8AWG wire.

The primary coil is a flat spiral, starting at 6in diameter and ending at 16in diameter after 6 turns (0.833in per turn). The full coil continues for an additional two turns to allow for tuning. The final diameter of the spiral was chosen to be about the same as the OD of the topload. Any bigger would just be inviting arcs to strike it, if they ever got that big. The total length of wire for the first six turns is about 17.3ft. Using the same wire gauge table, the resistance of this coil at DC would be 10.9mΩ. However, a if you treat the wire as a thin shell with the thickness equal to the 0.17mm skin depth, the resistance shoots up to 52.3mΩ. The 8AWG grounding wire is stranded, so it will probably be a little better than the thin shell approximation since it has more surface area. A safe bet might be 40mΩ.

Next, the three estimates of the spiral coil's inductance:

TCFormulas: 11.0μH

JavaTC: 10.8μH
FEMM: 11.8μH
Average: 11.2μH

Everything is in agreement, pretty much. For the flat coil simulation in FEMM, I assigned a six-turn winding to the flat coil winding area. FEMM treats the winding as evenly-distributed through that area, which is a good approximation of a spiral. I used a 200A test current, although it shouldn't matter much in air. Here's the FEMM-predicted flux distribution for the flat coil:

Primary Capacitor:

Finally, a component that I can just go look up in a catalog and buy! I will obviously have to choose the right type of capacitor and make sure its voltage and current ratings are sufficient. It might have to be a series/parallel combination of smaller/cheaper/more readily-available capacitors. But as for the value, I can pick whatever I want. 

That's why this component is chosen last: it takes whatever value is necessary for the primary circuit to have the same resonant frequency as the secondary circuit. Using 143kHz as the desired frequency and 11.2μH as the primary inductance, the required capacitance is 111nF. Since it's hard to find that exact value, and since capacitors are at best +/-10% accurate anyway, I chose 100nF as the size I will actually use.

100nF film capacitors come in a variety of flavors, differing in voltage/current rating and ESR. One example would be CDE 940C30P1K-F, rated to 3kVdc, 144A peak, and 8.1Arms, and the ESR is 10mΩ. I haven't gotten to the part where I figure out what voltage and current to expect at the primary, but no matter what I should be able to construct an [n x n] capacitor bank out of these to do the job. The current and voltage capability scale by n, but the final capacitance and ESR will remain unchanged.

Each capacitor in the bank will have a resistor across it, which serves two purposes. First, it bleeds current off the capacitor so that the bank discharges quickly if power is removed from the coil while the capacitors are still charged. Second, the resistors passively balance the voltages across capacitors that are in series.

Resonance:

The primary inductor, capacitor, and parasitic resistances combine to form another lightly-damped RLC resonant circuit. The goal is to tune this resonant circuit to the same natural frequency as the secondary resonant circuit. Since the capacitor value is fixed, tuning is accomplished by modifying the exact location of the end-tap on the spiral inductor. (It could be tweaked in small fractions of a turn.)

With that in mind, I set the primary inductance to 12.4μH to make the natrual frequency of the primary circuit also equal to 143kHz. I used a total series resistance of 60mΩ to account for the coil (including skin effect), capacitor ESR, and other stray resistances. The resulting bode plot looks like this:

It's very similar to the secondary, with about a +/-5% window for 20dB (10x) amplification. The important part is matching the primary's natural frequency to the secondary's, to get the most amplification possible.

The Coupling:

The primary and secondary coils form a loosely-coupled air-core transformer. Alternating flux created by the primary induces a voltage in the secondary which is further amplified by the secondary resonance. Only a small portion of the flux created by the primary current is linked by the secondary coil. This value is captured by the mutual inductance: the secondary flux linkage per unit primary amp. TCFormulas doesn't have a mutual inductance formula, but JavaTC and FEMM can calculate it:

TCFormulas: N/A

JavaTC: 82.3μH
FEMM: 85.1μH

Average: 83.7μH

Getting the mutual inductance from FEMM is easy: Drive the primary winding with 200A (or whatever), but measure the flux linkage of the secondary winding.

The mutual inductance is the secondary flux linkage, in Webers, divided by the primary current, in Amps (M = λ/I).

With the mutual, primary, and secondary inductances know, it's possible to calculate the tranformer's coupling coefficient, k, based on the formula k = M/sqrt(L1*L2). The coupling coefficient, a number between 0 and 1, is a measure of how strongly coupled the two coils are. Using 12.4μH for the primary inductance, 47.4mH for the secondary inductance, and 83.7μH for the mutual inductance, k = 0.109. This seems to be in the correct range for Tesla coils according to multiple sources.

With the mutual inductance known, it's also possible for the first time to get a ballpark estimate of the voltage generated by the coil. At 200A, the flux linkage of the secondary coil is λ = 83.7μH*200A = 16.7mWb. The AC voltage induced in the secondary coil is v = ω*λ = 2π*(143kHz)*16.7mWb =15.0kV. This voltage goes through one more stage of amplification, thanks to the secondary resonance peak. If the driving frequency is within the +/-5% margin for +20dB resonance peaking, a top load voltage of around 150kV could be possible.

It takes time for the primary current and the secondary voltage to build up, though. The bode plot really only applies to periodic steady-state. The 200A primary current is also only a guess at this point, based on a reasonable expectation of what the wire and the power devices can handle. To go any further, more details about the driver are needed.

Here's a look at the whole picture, combining the FEMM simulation outputs with the CAD model:

The right side has the magnetic simulation, showing the flux distribution created by current flowing in the primary coil. You can see that most of the flux misses the secondary coil entirely. That's the "loosely-coupled" bit. The left side has the electrostatic simulation, showing the potential created by the toroid.

The Driver:

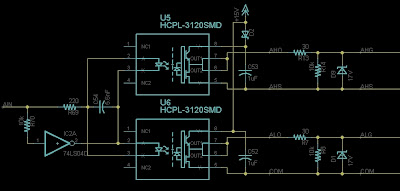
Working backwards from output to input, the last thing left is the driver: the power electronics that force the primary coil.This is the part I should be most familiar with: it's nothing more than an H-bridge, the same as what would be used to control a DC motor. The only difference is that this H-bridge needs to switch at around 150kHz, about 10x faster than the typical PWM frequency of a motor driver.

Most SSTC builders use IGBTs, and to be honest they are a better fit. For voltages higher than about 200-300V, the resistance of an equivalently-sized MOSFET limit the power it can handle. I'm much more comfortable with MOSFET gate drive, though, so I'm sticking with FETs and keepig the bus voltage low. The current plan is to use a 132V battery bus, made from two 66V packs that are split by a contactor when the coil is disarmed. In future revisions, I may also try a 170V bus derived from rectified mains.

There are a few advantages to working with a battery bus. One, no 60Hz AC ripple to filter out. The bus capacitors can be significantly smaller. Two, capable of higher power than a 120V outlet. Three, no extension cords and no unintentional ground loops. The main disadvantage is that you can't turn a battery off. Besides the pack-splitting contactor, it will require appropriate fusing.

On to my favorite part: FET shopping.

MOSFETs:

I made a list of just about every FET in the voltage and current rating I was looking for that was available on Digi-Key.

There are some powerful but very expensive IXYS MOSFETs in TO-247 and TO-264 packages. There are also some inexpensive ST and Infineon FETs with impressively good Figure-of-Merit (Rds*Cg), but they are in small packages. In the end, I chose the IR FETs that were a good balance of cost, FoM, and thermal capability. These would be the 200V IRFP4668, if limited to the 132V battery bus, or the 250V IRFP4768, if using a 170V rectified mains bus.

The IRFP4668 is a particularly impressive FET. It has an on-state resistance of  8.0mΩ, so the voltage drop at 200A is 1.6V, significantly lower than the Vce on an equivalent IGBT at that current. (Granted, an equivalent IGBT would be rated to 600V.) The total gate charge, 160nC, is high but not insane. The only thing that is somewhat lacking about this FET is the intrinsic diode. Its reverse recovery specs are not very good, especially at the high di/dt values I'm anticipating. To make up for the MOSFET's underachiever diode, I'll be pairing it with an ultrafast APT100S20B Schottky diode. This should help in the deadtime between the driving FET turn-off and the freewheeling FET turn-on. It also move a bit of the switching loss out of the FET.

I found that I could fit two FETs and one diode per leg of a bridge all within a standard 4"x3" frEAGLE maximum board size:

The center rails are the DC bus, positive and negative from the battery. The outer rails are the outputs for each side of the primary coil. Five 18mm-diameter electrolytic capacitors should allow for at least 2,000uF at 200V rating. At 132V, this much bus capacitance would store 17.4J. Comparing this to a worst-case current pulse of 200A at 132V for 100us (2.64J) suggests that it should be enough. (The true current won't be a rectangular pulse.) If not, it's easy to add more off-board.

Gate Drive:

I'm departing a bit from the gate drive solutions I've seen in MITERS coils, not because I think I can do better but because I want to stick with drivers that I know. For a good review of high power gate drivers, you can check out Bayley's or Tyler's posts about them. They tend to use custom full-bridge drivers with Gate Drive Transformers (GDTs) to achieve final isolation between the gate drive hardware and the gates.

For almost all of my high power (>1kW) motor controllers, I use optically-isolated gate drivers. I started doing this with Cap Kart. With them, it's easy to make modular half-bridges with passive dead-time and shoot through protection built in. The half-bridge driver looks like this:

Note: This is NOT the driver to be used on this coil. Just an example.

It's got two optically-isolated gate drivers with the input LEDs wired in anti-parallel so that only one or the other can be on at any given time (inherent shoot-through protection). There's a capacitor between the LEDs and a current-limiting resistor at the input. These form an RC filter which sets the delay time between the turn-off of one LED and the turn-on of the other (passive deadtime insertion). The output is a typical bootstrapped half-bridge drive run on 15V.

The input signal can be inverted in software or hardware to drive the opposite polarity for the low-side. The input has no electrical connection to the power electronics. As far as the input signal generator is concerned, it's driving an LED. It's actually a relatively low-impedance signal, since it takes several mA to turn on an LED. This makes it significantly more noise-immune than a logic input. It also allows the input signal to be tri-stated, which has the result of turning off both the high side and the low side LED, since no drive current flows.

Now the bad news: Optically-isolated gate drivers are slow and relatively low power. Well, maybe I can solve at least one of those problems. Back when I was designing DirectDrive, my large motor controller, I came across a relatively new gate drive optocoupler, the ACNW-3190, made by Avago. It has a 5.0A maximum output and I thought it was pin-compatible with the HCPL-3120 that I've used in many other designs. In fact it would be pin-compatible if it was't a fat 400mil DIP instead of the normal 300mil DIP. Anyway, I have a rail of the ACNW-3190 that's been sitting around since I discovered they won't fit in DirectDrive. They should make nice gate drivers for this project.

5A gate drive should be plenty for 150kHz with the chosen FETs. A ballpark estimate of the switching time can be found by dividing the total gate charge (160nC) by half the gate drive current, 2.5A. This gives 64ns, which is less than 1% of the switching period. A simulation with real component values would give a better estimate, but it seems fine.

The bigger problem with gate drive optocouplers is their propagation delay times, typically 300-500ns. This is about 7.5% of a switching cycle, or 27º of phase lag, at 150kHz. If I were attempting to achieve Zero Current Switching (ZCS) based on current sensor feedback, it would be hard (but probably not impossible) to make this driver work. Instead, I'm abandoning soft-switching altogether and driving the input open-loop.

Input Signal Generator:

Instead of a hardware-based ZCS feedback circuit, I am planning to generate a fixed-frequency input signal directly from a microcontroller (STM32F103C4 running at 72MHz). The input signal would be two sets of ~150kHz square waves lasting for a small number of cycles. The exact frequency of the square waves is adjustable to within the timer resolution at 72MHz. This works out to a minimum frequency step of about 0.3kHz around 150kHz. This input event, called a "pulse", would consist of a small number (10-15?) of square wave periods, which will hopefully establish resonance and create a spark. This has a number of pros and cons that I can already think of, and probably more of each that I can't think of.

Pros: It's not possible for it to go unstable because of reverse or broken feedback. It's one more adjustment knob to turn for tuning - you can dial in an exact drive frequency even if the primary itself is slightly out of tune. It's possible to vary the duty cycle or relative phase of the drive signals as well for variable power control.

Cons: It can and will hard-switch, although hopefully not at peak current. It's one extra tuning step. The signal-generating microcontroller and the lines from it to the gate drivers may be susceptible to EMI. (Normally, the control line would be an optical interrupter.)

Hopefully the Pros outweigh the Cons and I can get past the initial "does it blow up" stage. If so, the direct input signal generation should make high-level control of pulse length and pulse frequency very easy. And, by generating the pulses at a specific frequency (or frequencies), the coil can become musical!

SPICE Sims:

Last, as a way of putting all of the different parts into a single simulation, I turned to SPICE, specifically the free version LTspice. LTspice is a circuit simulator that can handle simple passives as well as complicated models of transistors. In fact, I was able to find a SPICE model of the IRFP4668 on the IRF website. The model combines all of the estimations of circuit parameters made in the previous sections.

The primary, driven by the full-bridge of FETs, is on the left. The secondary with optional streamer loading path, is on the right. The entire bridge is fed by a 2000uF capacitor initially charged to 132V. (It's a single-pulse simulation.) The drive voltages, which are the outputs of each half bridge, look like this:

Here, the half-bridge outputs are exactly 180º out of phase and at about 36% duty cycle. 180º out of phase and 50% duty cycle would be the maximum drive. By adjusting the duty cycle between 0% and 50%, or by taking the two waveforms more or less out of phase, the overall drive power can be varied.

Driving the coil at exactly 143kHz, the natural frequency of the primary and secondary circuits, doesn't quite work. Here's what the primary and secondary voltage/current waveforms look like at 143kHz drive frequency and 50% duty cycle:

Primary

Secondary

Resonance is definitely happening, but over the course of one "pulse" (here, 15 cycles), the primary rings up to 1.5kV and 120A, but then gets pushed back down nearly to zero before ringing up again. This beat frequency results from the coupling between the primary and the secondary. The secondary in this case reaches about 160kV. 

But better results can be achieved by taking into account "frequency splitting". This suggests driving the coupled system at 143kHz / sqrt(1±k) = {136kHz, 151kHz}. Might as well try both. First. 151kHz:

Primary

Secondary

There are still some interesting dynamics, but for the same number of cycles (15), the primary now reaches over 3kV and 300A! The secondary reaches over 200kV. Next, 136kHz drive:

Primary

Secondary

Simiarly results. About 3kV and 250A on the primary, and 200kV on the secondary. So driving at either of the two split frequencies should be okay. 136kHz will be marginally easier on the FETs and gate drive, so maybe I'll start there. In truth, the actual resonant frequencies will probably be very different when I build it, so I'll have to hunt around for an optimum point both by tuning the primary inductor and by varying the drive frequency. But, doing the detailed design at least gives me confidence that I'll be in the right ballpark for everything.

I'm told the next step involves a lot of winding.......